Browse By Unit
Unit 4 Overview: Functions Involving Parameters, Vectors, & Matrices
1 min read•june 18, 2024
4.0 Functions Involving Parameters, Vectors, and Matrices
Last but not least! AP Precalculus’ Unit 4 focuses on several important topics involving another group of functions, including functions involving parameters, vectors, and matrices. Like units 1 to 3, these topics will challenge and enrich your understanding of mathematical concepts and help you develop critical thinking skills. One thing to note is that this unit is not required, which means that the topics covered here are technically not on the exam. Phew! 😪
Even so, these topics are interesting to explore in a sense that they provide the foundation to higher level math concepts: calculus, linear algebra, differential equations, you name it! Without further ado, let’s dive into the big picture for each of them. 😉
Unit Breakdown
Parametric Functions and Applications
Parametric functions are mathematical functions that are defined using parameters instead of variables. They can be used to model a variety of real-world situations, such as the movement of a particle in space. In this unit, you will learn how to graph parametric functions and analyze their properties, including rates of change and tangent lines. 🚀
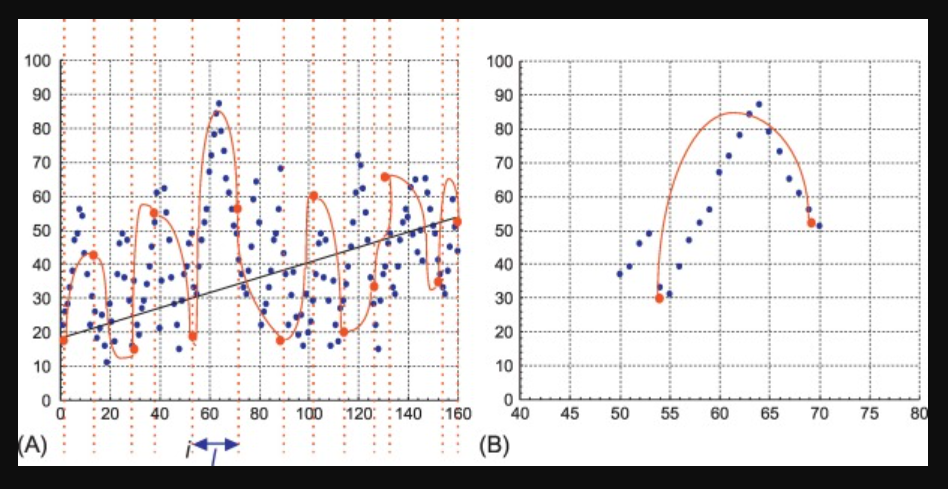
Source: Data Analytics
Parametric functions modeling planar motion are a special type of parametric function that describe the motion of a point in a two-dimensional plane. ✈ You will learn how to analyze the motion of a point and how to use the functions to describe the path of the point over time.
The relationship between parametric functions and rates of change is another key concept. You will be introduced to the concept of calculating the rate of change for a parametric function and how this information can be used to better understand the behavior of the function.
The rate of change gives insight into how the output of a function is changing over time, which is important in many real-world applications. By learning how to calculate the rate of change of a parametric function, you will be able to analyze and interpret the behavior of the function in more detail. 🤓
Parametrically defined circles and lines are also important topics in this unit. You will learn how to define circles and lines using parameters and how to graph these shapes. This will include learning how to translate these definitions into mathematical equations and how to graph the shapes using these equations. Understanding how to define and graph circles and lines using parameters is an important part of understanding mathematical modeling. 🔵
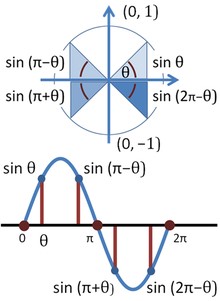
Source: Trig Identities
Implicitly Defined Functions and Conic Sections
Implicitly defined functions are mathematical functions that are defined without explicitly stating the independent variable. Instead, the relationship between the independent and dependent variables is defined implicitly through an equation. These functions are useful in modeling real-world situations where the relationship between the variables is not easily represented by a traditional function. 📌
You will learn how to graph implicitly defined functions and how to use these functions to model real-world situations. This will involve learning how to translate the implicit equation into a graphical form and how to interpret the resulting graph. 📈
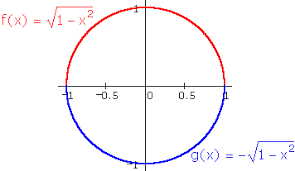
Source: WMueller
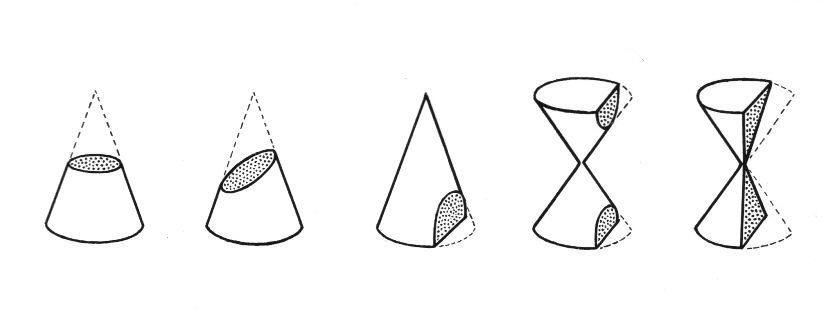
Conic sections are a special type of implicitly defined function that are used to model a variety of shapes, including circles, ellipses, parabolas, and hyperbolas. These shapes are commonly found in real-world applications, such as in engineering and physics, and are important to understand. In this unit, you will learn how to graph conic sections and how to use them to model real-world situations. 🔔
Parametrization of implicitly defined functions is an important topic in this unit as well. You will learn how to define implicitly defined functions using parameters and how to graph these functions. 🌶
Source: Wiktionary
This will involve learning how to translate the implicit equation of a function into a parametric form and how to graph the resulting parametric function. Understanding how to parametrize implicitly defined functions is important in modeling real-world situations and will allow you to analyze the behavior of these functions in more detail. 🥥
Vectors and Vector-Valued Functions
Vectors are mathematical objects that play a fundamental role in various fields, including physics and engineering. A vector can be used to describe the magnitude and direction of a physical quantity, such as velocity, force, or displacement. ↔️
In this unit, you will learn how to use vectors to describe motion, to find the distance and angle between two points, and to perform other mathematical operations. This will involve learning how to add and subtract vectors, to find the magnitude and direction of a vector, and to calculate the dot product and cross product of vectors. ⏺
To spice things up, vector-valued functions are functions that take a scalar value as input and produce a vector as output. These functions are useful in modeling real-world situations where the relationship between variables is best described as a vector. You will learn how to graph vector-valued functions and how to use them to model real-world situations. ↗️
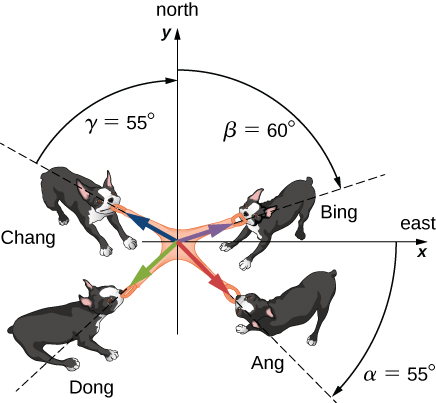
Source: Lumen Learning
You will also learn how to use vector-valued functions to describe motion, to find the position and velocity of a point over time, and to model other real-world situations. 🌎
Matrices
Matrices are arrays of numbers that can be used to represent linear transformations and to model real-world situations. In this unit, you will learn how to perform operations with matrices, including addition, subtraction, and multiplication, and how to find the inverse and determinant of a matrix. ♾️
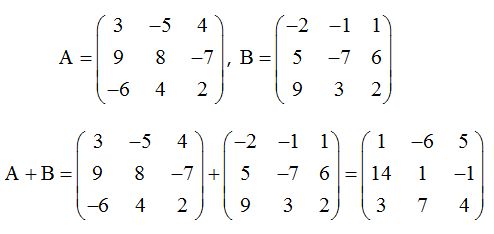
Source: Weebly
Linear transformations and matrices are closely related. You will learn how to use matrices to represent linear transformations and how to analyze the properties of linear transformations.
Matrices as functions are a special type of function that take a vector as input and produce a vector as output. You will learn how to use matrices as functions to model real-world situations and how to analyze their properties. 🔎
In matrices modeling contexts, you will learn how to use matrices to model real-world situations, such as data analysis and computer graphics. You will also learn how to use matrices to solve real-world problems, such as optimization and linear programming, down the road (years later after this course), hopefully! 🤖
<< Hide Menu
Unit 4 Overview: Functions Involving Parameters, Vectors, & Matrices
1 min read•june 18, 2024
4.0 Functions Involving Parameters, Vectors, and Matrices
Last but not least! AP Precalculus’ Unit 4 focuses on several important topics involving another group of functions, including functions involving parameters, vectors, and matrices. Like units 1 to 3, these topics will challenge and enrich your understanding of mathematical concepts and help you develop critical thinking skills. One thing to note is that this unit is not required, which means that the topics covered here are technically not on the exam. Phew! 😪
Even so, these topics are interesting to explore in a sense that they provide the foundation to higher level math concepts: calculus, linear algebra, differential equations, you name it! Without further ado, let’s dive into the big picture for each of them. 😉
Unit Breakdown
Parametric Functions and Applications
Parametric functions are mathematical functions that are defined using parameters instead of variables. They can be used to model a variety of real-world situations, such as the movement of a particle in space. In this unit, you will learn how to graph parametric functions and analyze their properties, including rates of change and tangent lines. 🚀

Source: Data Analytics
Parametric functions modeling planar motion are a special type of parametric function that describe the motion of a point in a two-dimensional plane. ✈ You will learn how to analyze the motion of a point and how to use the functions to describe the path of the point over time.
The relationship between parametric functions and rates of change is another key concept. You will be introduced to the concept of calculating the rate of change for a parametric function and how this information can be used to better understand the behavior of the function.
The rate of change gives insight into how the output of a function is changing over time, which is important in many real-world applications. By learning how to calculate the rate of change of a parametric function, you will be able to analyze and interpret the behavior of the function in more detail. 🤓
Parametrically defined circles and lines are also important topics in this unit. You will learn how to define circles and lines using parameters and how to graph these shapes. This will include learning how to translate these definitions into mathematical equations and how to graph the shapes using these equations. Understanding how to define and graph circles and lines using parameters is an important part of understanding mathematical modeling. 🔵

Source: Trig Identities
Implicitly Defined Functions and Conic Sections
Implicitly defined functions are mathematical functions that are defined without explicitly stating the independent variable. Instead, the relationship between the independent and dependent variables is defined implicitly through an equation. These functions are useful in modeling real-world situations where the relationship between the variables is not easily represented by a traditional function. 📌
You will learn how to graph implicitly defined functions and how to use these functions to model real-world situations. This will involve learning how to translate the implicit equation into a graphical form and how to interpret the resulting graph. 📈

Source: WMueller
Conic sections are a special type of implicitly defined function that are used to model a variety of shapes, including circles, ellipses, parabolas, and hyperbolas. These shapes are commonly found in real-world applications, such as in engineering and physics, and are important to understand. In this unit, you will learn how to graph conic sections and how to use them to model real-world situations. 🔔
Parametrization of implicitly defined functions is an important topic in this unit as well. You will learn how to define implicitly defined functions using parameters and how to graph these functions. 🌶

Source: Wiktionary
This will involve learning how to translate the implicit equation of a function into a parametric form and how to graph the resulting parametric function. Understanding how to parametrize implicitly defined functions is important in modeling real-world situations and will allow you to analyze the behavior of these functions in more detail. 🥥
Vectors and Vector-Valued Functions
Vectors are mathematical objects that play a fundamental role in various fields, including physics and engineering. A vector can be used to describe the magnitude and direction of a physical quantity, such as velocity, force, or displacement. ↔️
In this unit, you will learn how to use vectors to describe motion, to find the distance and angle between two points, and to perform other mathematical operations. This will involve learning how to add and subtract vectors, to find the magnitude and direction of a vector, and to calculate the dot product and cross product of vectors. ⏺
To spice things up, vector-valued functions are functions that take a scalar value as input and produce a vector as output. These functions are useful in modeling real-world situations where the relationship between variables is best described as a vector. You will learn how to graph vector-valued functions and how to use them to model real-world situations. ↗️

Source: Lumen Learning
You will also learn how to use vector-valued functions to describe motion, to find the position and velocity of a point over time, and to model other real-world situations. 🌎
Matrices
Matrices are arrays of numbers that can be used to represent linear transformations and to model real-world situations. In this unit, you will learn how to perform operations with matrices, including addition, subtraction, and multiplication, and how to find the inverse and determinant of a matrix. ♾️
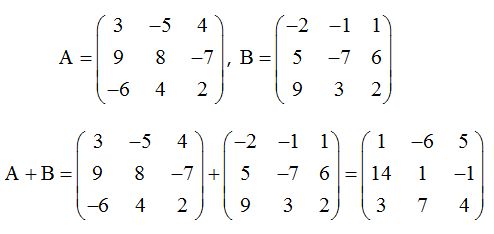
Source: Weebly
Linear transformations and matrices are closely related. You will learn how to use matrices to represent linear transformations and how to analyze the properties of linear transformations.
Matrices as functions are a special type of function that take a vector as input and produce a vector as output. You will learn how to use matrices as functions to model real-world situations and how to analyze their properties. 🔎
In matrices modeling contexts, you will learn how to use matrices to model real-world situations, such as data analysis and computer graphics. You will also learn how to use matrices to solve real-world problems, such as optimization and linear programming, down the road (years later after this course), hopefully! 🤖

© 2024 Fiveable Inc. All rights reserved.