Browse By Unit
Jesse
Jesse
4.8 Vectors
Vectors are mathematical objects—directed line segments—that have both a magnitude (size) and a direction. They can be used to represent things like velocity, force, and acceleration in physics, or they can be used in other branches of mathematics like geometry and linear algebra. 🏹
A common way to represent a vector is by an arrow pointing in a certain direction, with the length of the arrow representing the magnitude of the vector. ↗️
- The point at which the vector starts is called the tail
- The point at which it ends is known as the head.

Image Courtesy of Math Insight
📸 Representing Vectors
A vector can be represented in a two-dimensional plane, such as the xy-plane, using two components. The vector is defined by two points, and , where the point is the tail and is the head. 🛩️
The vector can be identified by two scalars a and b, where a represents the change in the x-coordinate () and b represents the change in the y-coordinate (). The vector can be written in the form of , where a and b are the components of the vector. A special case of a vector is the zero vector, , which occurs when and are the same point and the magnitude of the vector is zero. 🤓

Image Courtesy of Math Insight
The vector's direction is parallel to the line connecting the origin to the point (a, b), and its magnitude is the square root of the sum of the squares of its components. 💟
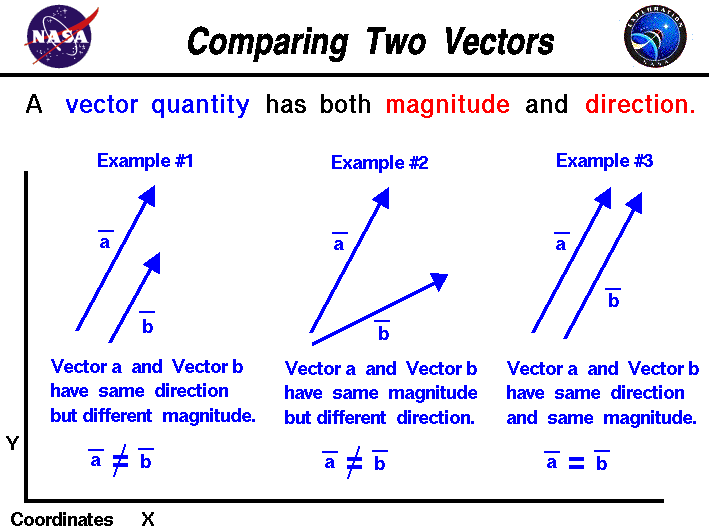
Image Courtesy of NASA

Image Courtesy of Khan Academy
⚒ Vector Operations
✖️ Multiplication (Constant and Vector)
When a constant is multiplied by a vector, the resulting vector has the same direction as the original vector, but its magnitude (size) is scaled by the constant. Each component of the new vector is found by multiplying the corresponding component of the original vector by the constant. 🦤
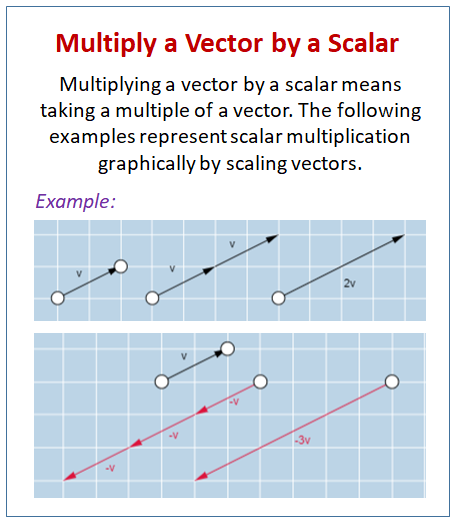
Image Courtesy of Online Math Learning
➕ Addition
The sum of two vectors in two-dimensional space is a new vector that can be obtained by adding the corresponding components of the original vectors. ✌️
The new vector can be visualized as the vector that starts at the tail of the first vector and ends at the head of the second vector when the tail of the second vector is placed at the head of the first vector. It can be also represented geometrically as the diagonal of a parallelogram formed by the vectors. 🏖️
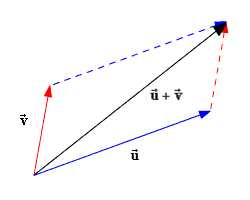
Image Courtesy of Varsity Tutors
🔘 Dot Products
The dot product of two vectors is a scalar value that represents the degree of similarity between the vectors. It is calculated as the sum of the products of the corresponding components of the two vectors. 🔢

Image Courtesy of Master Data Science
The dot product formula for two vectors A and B is:
For example, if we have a 2D vector and a 2D vector , we can calculate their dot product as:
The dot product of two vectors is a scalar value, which tells us the degree of similarity between them. A dot product of 0 means that the vectors are orthogonal, while a positive dot product indicates that the vectors point in a similar direction. A negative dot product means that the vectors point in opposite directions. 👾
The dot product measures how similar the vectors are to each other, with a value of zero indicating that the vectors are perpendicular. In other words, if the dot product of two nonzero vectors is zero, it means that the angle between the two vectors is 90 degrees and the vectors are orthogonal to each other. This is because when two vectors are perpendicular, the cosine of the angle between them is zero, and therefore their dot product is also zero. 🧐
✔️ Unit Vectors
A unit vector is a vector that has a magnitude or length of 1. This type of vector is useful in many mathematical and physical contexts because it allows for the direction of a vector to be specified without reference to its magnitude. 1️⃣
To find a unit vector in the same direction as a given nonzero vector, one can take the original vector and multiply it by the reciprocal of its magnitude. This process effectively "shrinks" the vector down to a length of 1 while preserving its direction. 🤓
For example, if a vector has a magnitude of 5, its reciprocal is 1/5, and multiplying the vector by 1/5 will result in a unit vector in the same direction as the original vector.
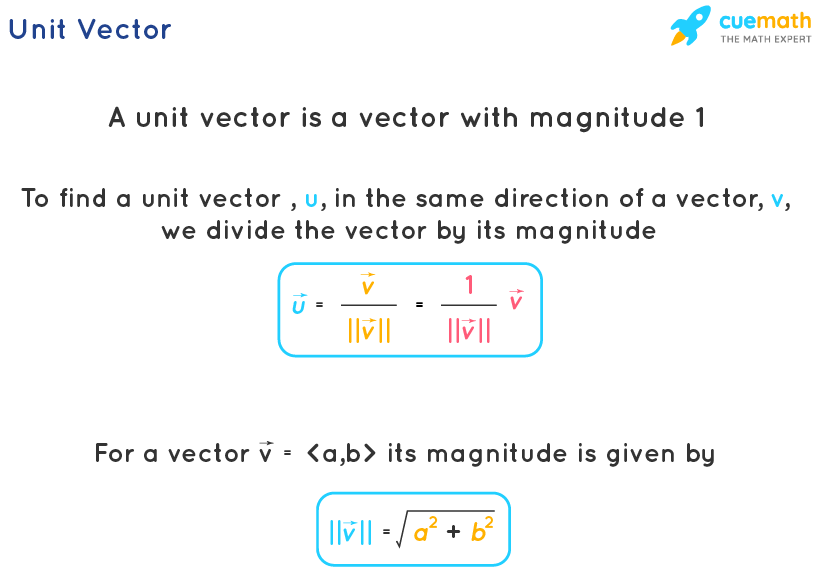
Image Courtesy of Cuemath
A vector in two-dimensional space, represented by the ordered pair , can be expressed as a linear combination of the standard unit vectors i and j. The vector can be written as , where i and j are unit vectors that point along the x-axis and y-axis, respectively. 🚲
The vector i is equal to , meaning that it has a magnitude of 1 and points only in the positive x-direction. Similarly, the vector j is equal to , meaning that it has a magnitude of 1 and points only in the positive y-direction. By expressing a vector in this form, it becomes easier to understand its properties like magnitude, direction and also perform mathematical operations on it. 〽️
〰️ Appendix: Side Lengths and Angles
The Law of Sines and the Law of Cosines are two important mathematical formulas that are used to solve problems involving triangles. 🫰
The Law of Sines
The Law of Sines states that for any triangle with side lengths a, b, and c, and angles A, B, and C opposite those sides, the ratio of the length of a side to the sine of the angle opposite that side is the same for all three sides of the triangle. This relationship can be written as:

Image Courtesy of Clark University
The Law of Cosines
The Law of Cosines, on the other hand, relates the lengths of the sides of a triangle to the cosine of one of its angles.
The Law of Cosines states that for any triangle with side lengths a, b, and c, and angles A, B, and C opposite those sides, the sum of the squares of the lengths of any two sides of the triangle is equal to the square of the length of the third side, minus twice the product of the length of the third side and the cosine of the angle opposite that side. This relationship can be written as:
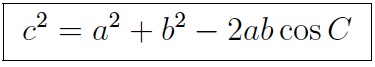
Image Courtesy of Clark University
Applying the Laws of Sines and Cosines
Both the Law of Sines and the Law of Cosines can be used to determine the side lengths and angles of triangles formed by vector addition, as well as to check the consistency of information given in a problem. 🟰
In addition, these laws can also be used to find if a set of measurements correspond to a valid triangle, by checking the triangle inequality theorem, which states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side. 📐
<< Hide Menu
Jesse
Jesse
4.8 Vectors
Vectors are mathematical objects—directed line segments—that have both a magnitude (size) and a direction. They can be used to represent things like velocity, force, and acceleration in physics, or they can be used in other branches of mathematics like geometry and linear algebra. 🏹
A common way to represent a vector is by an arrow pointing in a certain direction, with the length of the arrow representing the magnitude of the vector. ↗️
- The point at which the vector starts is called the tail
- The point at which it ends is known as the head.

Image Courtesy of Math Insight
📸 Representing Vectors
A vector can be represented in a two-dimensional plane, such as the xy-plane, using two components. The vector is defined by two points, and , where the point is the tail and is the head. 🛩️
The vector can be identified by two scalars a and b, where a represents the change in the x-coordinate () and b represents the change in the y-coordinate (). The vector can be written in the form of , where a and b are the components of the vector. A special case of a vector is the zero vector, , which occurs when and are the same point and the magnitude of the vector is zero. 🤓

Image Courtesy of Math Insight
The vector's direction is parallel to the line connecting the origin to the point (a, b), and its magnitude is the square root of the sum of the squares of its components. 💟

Image Courtesy of NASA

Image Courtesy of Khan Academy
⚒ Vector Operations
✖️ Multiplication (Constant and Vector)
When a constant is multiplied by a vector, the resulting vector has the same direction as the original vector, but its magnitude (size) is scaled by the constant. Each component of the new vector is found by multiplying the corresponding component of the original vector by the constant. 🦤

Image Courtesy of Online Math Learning
➕ Addition
The sum of two vectors in two-dimensional space is a new vector that can be obtained by adding the corresponding components of the original vectors. ✌️
The new vector can be visualized as the vector that starts at the tail of the first vector and ends at the head of the second vector when the tail of the second vector is placed at the head of the first vector. It can be also represented geometrically as the diagonal of a parallelogram formed by the vectors. 🏖️

Image Courtesy of Varsity Tutors
🔘 Dot Products
The dot product of two vectors is a scalar value that represents the degree of similarity between the vectors. It is calculated as the sum of the products of the corresponding components of the two vectors. 🔢

Image Courtesy of Master Data Science
The dot product formula for two vectors A and B is:
For example, if we have a 2D vector and a 2D vector , we can calculate their dot product as:
The dot product of two vectors is a scalar value, which tells us the degree of similarity between them. A dot product of 0 means that the vectors are orthogonal, while a positive dot product indicates that the vectors point in a similar direction. A negative dot product means that the vectors point in opposite directions. 👾
The dot product measures how similar the vectors are to each other, with a value of zero indicating that the vectors are perpendicular. In other words, if the dot product of two nonzero vectors is zero, it means that the angle between the two vectors is 90 degrees and the vectors are orthogonal to each other. This is because when two vectors are perpendicular, the cosine of the angle between them is zero, and therefore their dot product is also zero. 🧐
✔️ Unit Vectors
A unit vector is a vector that has a magnitude or length of 1. This type of vector is useful in many mathematical and physical contexts because it allows for the direction of a vector to be specified without reference to its magnitude. 1️⃣
To find a unit vector in the same direction as a given nonzero vector, one can take the original vector and multiply it by the reciprocal of its magnitude. This process effectively "shrinks" the vector down to a length of 1 while preserving its direction. 🤓
For example, if a vector has a magnitude of 5, its reciprocal is 1/5, and multiplying the vector by 1/5 will result in a unit vector in the same direction as the original vector.

Image Courtesy of Cuemath
A vector in two-dimensional space, represented by the ordered pair , can be expressed as a linear combination of the standard unit vectors i and j. The vector can be written as , where i and j are unit vectors that point along the x-axis and y-axis, respectively. 🚲
The vector i is equal to , meaning that it has a magnitude of 1 and points only in the positive x-direction. Similarly, the vector j is equal to , meaning that it has a magnitude of 1 and points only in the positive y-direction. By expressing a vector in this form, it becomes easier to understand its properties like magnitude, direction and also perform mathematical operations on it. 〽️
〰️ Appendix: Side Lengths and Angles
The Law of Sines and the Law of Cosines are two important mathematical formulas that are used to solve problems involving triangles. 🫰
The Law of Sines
The Law of Sines states that for any triangle with side lengths a, b, and c, and angles A, B, and C opposite those sides, the ratio of the length of a side to the sine of the angle opposite that side is the same for all three sides of the triangle. This relationship can be written as:

Image Courtesy of Clark University
The Law of Cosines
The Law of Cosines, on the other hand, relates the lengths of the sides of a triangle to the cosine of one of its angles.
The Law of Cosines states that for any triangle with side lengths a, b, and c, and angles A, B, and C opposite those sides, the sum of the squares of the lengths of any two sides of the triangle is equal to the square of the length of the third side, minus twice the product of the length of the third side and the cosine of the angle opposite that side. This relationship can be written as:
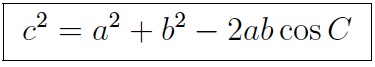
Image Courtesy of Clark University
Applying the Laws of Sines and Cosines
Both the Law of Sines and the Law of Cosines can be used to determine the side lengths and angles of triangles formed by vector addition, as well as to check the consistency of information given in a problem. 🟰
In addition, these laws can also be used to find if a set of measurements correspond to a valid triangle, by checking the triangle inequality theorem, which states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side. 📐

© 2024 Fiveable Inc. All rights reserved.